Recently, Dominik Scheder, an associate professor at the Department of Computer Science and Engineering, School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, made progress on a k-SAT, an important problem in theoretical computer science. In particular, he obtained the to date best time complexity for this well-studied NP-complete problem. His paper, "PPSZ is better than you think", has been accepted at the 62nd Annual IEEE Symposium on Foundations of Computer Science (FOCS 2021), one of the few top conferences in theoretical computer science.
This is the first result showing that the (relatively) simple 1998 analysis of PPSZ is sub-optimal. Adding to its elegance, it achieves the new bound without any change to the algorithm, focusing only on a more thorough analysis. It thus opens the door for further research into the true time complexity of this algorithm.
This work has been funded by the National Natural Science Foundation of China under the project "Algorithms for boolean satisfiability and the complexity of monotone boolean functions".
The Boolean satisfiability problem (SAT) is maybe the most prominent member of NP, a class of important (and often difficult) decision and optimization problems.
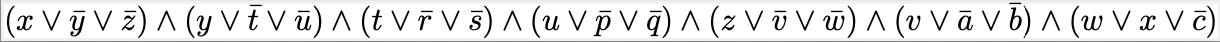
Caption: An example of a 3-CNF formula
The algorithm PPSZ referred to in the title of the paper, introduced in 1998 by Paturi, Pudlak, Saks, and Zane, rests on the idea of efficiently encoding a satisfying assignment . We encode by first putting the Boolean variables in some random order and then outputting the bits in that order. The twist is that we skip the bit if its value can be inferred by a certain local rule. This encoding is easily reversible by an equally efficient decoder. One turns this into a probabilistic SAT algorithm by feeding the decoder random bits. With probability 2^{ - codelength}, the first <codelength> random bits coincide with the true encoding of , and the decoder will correctly recover .
The original analysis by Paturi, Pudlak, Saks, and Zane rests on analyzing the expected codelength of alpha. A recent paper by Hansen, Kaplan, Zamir, and Zwick (STOC 2019) obtains an improved algorithm by feeding the decoder slightly biased random bits.
The presented paper improves the analysis of PPSZ rather than the algorithm itself and achieves an exponentially improved bound on its time complexity. This is done in two steps: first, one shows that if we choose the variable order not uniformly at random but from a carefully crafted distribution, one obtains an encoding that is significantly shorter on expectation. Second, one can show that instead of actually sampling from this distribution (which cannot be done efficiently), it is enough to simply "pretend" that the algorithm draws its randomness from it. The second step sounds mysterious but turns out to be mathematically very simple. The technical detail lies in the analysis of certain extinction events in rooted trees.
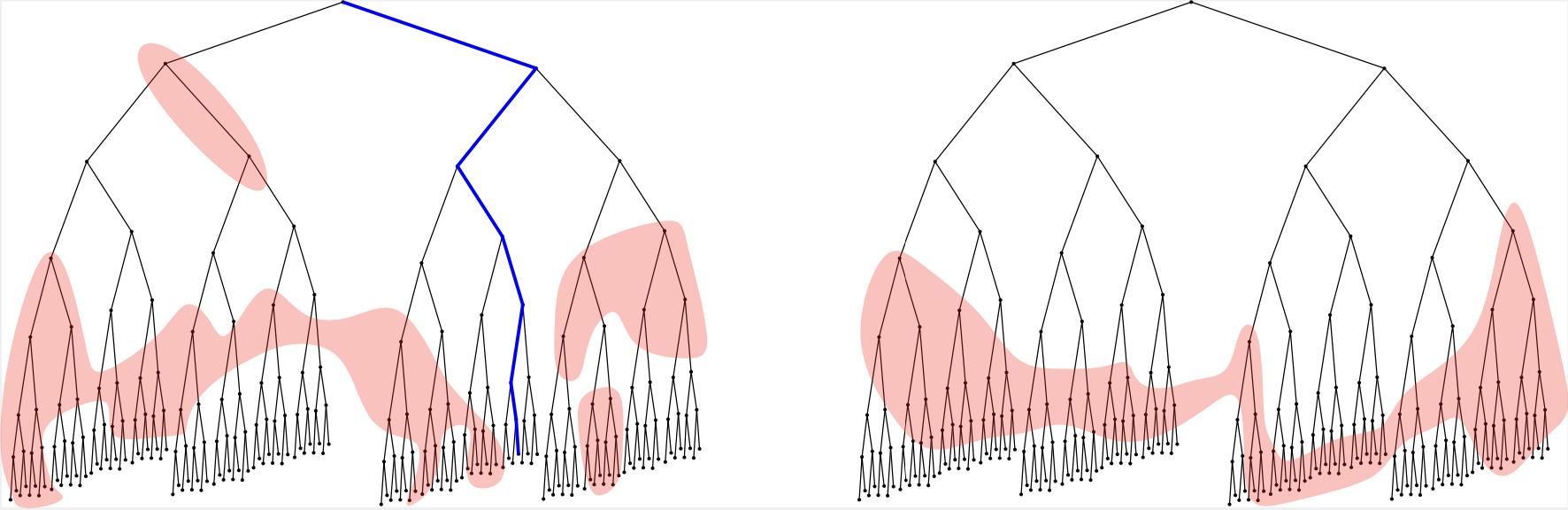
Caption: Extinction in binary trees: the left tree has a surviving path, avoiding the red vertices; in the right tree, no such path exists, so extinction occurs

Dominik Scheder is a tenure-track associate professor at Shanghai Jiao Tong University. He obtained his PhD from ETH Zurich in 2011. After positions as a postdoctoral researcher in Aarhus, Denmark, the Simons Institute at UC Berkeley, and at Tsinghua University, he joined our department in 2014.